前言

P2感觉比P1的难度大了很多，内部实现基本完全由自己决定，刚上手的时候没有指引有点手足无措，但同时也代表了实现的方式可以非常自由。

真的是很磨练人的一个project, 不过听说奇数年是实现hashmap要友好一些，有机会可以试一下

Task1

Task 1是要实现pages类，要改动的有三个文件b_plus_tree_page 、b_plus_internal_page、b_plus_leaf_page

没什么好说的，先把接口补全，之后的task还是需要对内容进行改动的，这里主要是理解他们之间的关系，方便之后的完成

结构如下：

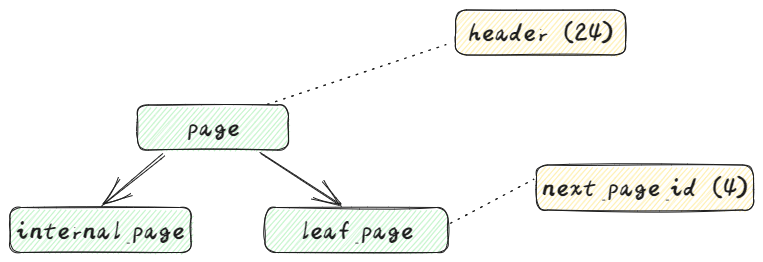
leaf_page比internal_page多一个next_page_id的字段

B+树page的整体结构:

notes

要注意的点主要有两个：1.GetMinSize() 2.array_

  • GetMinSize()

获取minsize，其实就是半满条件，但是leaf_page和internal_page对半满的定义不同，可以参照一下官方给的可视化工具BusTub B+Tree Printer

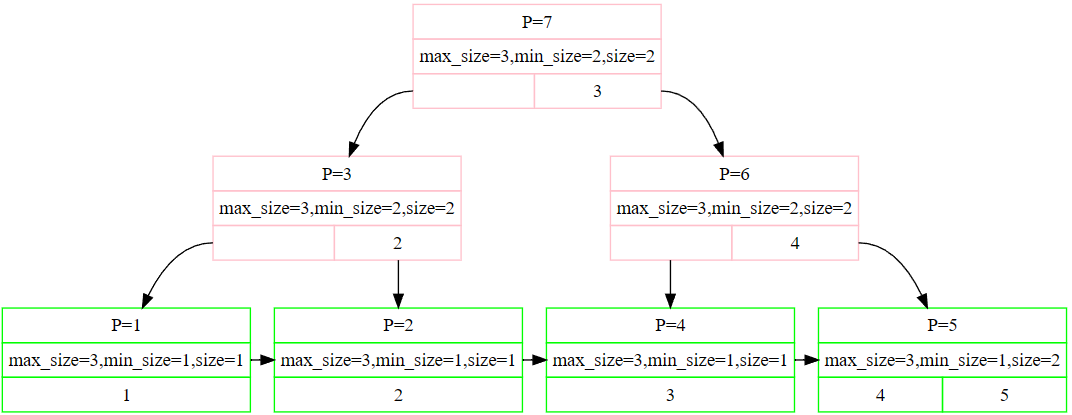
可以看到在max_size都是3的情况下，内部节点的min_size为2, 而叶节点的min_size是1，所以我们在完善GetMinSize()函数的时候要注意区分内部节点和叶子节点，内部节点为(max_size + 1) / 2, 叶子节点为max_size / 2

  • array_

array_其实就是用来存储键值对的容器，这里容易产生疑问的点在于array_[1]只能存一个KV吗？

这里的array_其实是一个柔性数组，允许你在结构体的末尾定义一个数组，其大小可以在运行时动态确定。

简单来说，初始化一个类对象时，无法确定该数组要设置的大小，但知道类对象的大小，就可以利用柔性数组，它可以自动填充未被其他变量使用的内存从而确定长度。柔性数组必须是类中最后一个成员。

Task2

task2要求我们实现B+树整个数据结构，整个project的重点

一共需要实现三个函数GetValue、Insert、Remove

难度也是 GetValue > Insert > Remove

GetValue

查找的流程比较简单，无非是找到key值、向下遍历。其中主要注意的是KeyComparator,这个类是专门用来比较key值大小的比较器，实现在generic_key文件中，具体实现方式可以自行查阅，简单来说就是

1
2
3
4
5
6
7
8
Keycomparator comparator_;
if (key1 < key2) {
	comparator_(key1, key2) < 0;	//key1小于key2，比较结果为负
} else if (key1 > key2) {
    comparator_(key1, key2) > 0;	//key1大于key2，比较结果为正
} else {
    comparator_(key1, key2) = 0;	//key1等于key2，比较结果为0
}

还有要注意的是叶子节点与内部节点的区别

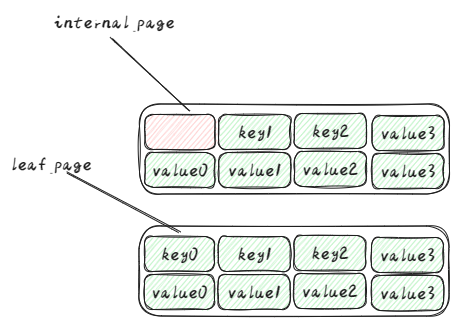
内部节点的第一个key是无效的，而叶子节点不是

并且内部节点的value值指向的是下一个节点，有可能是内部节点，有可能是叶子节点；而叶子节点的value则是数据本身，两者在value上也有区别

理清其中的关系之后，就可以开始实现了

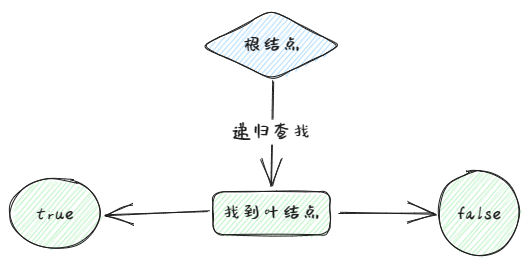
通过Findleaf()函数遍历整个树，从根节点开始查找，直到找到叶节点，再在叶节点中寻找对应key，找到返回true，并赋值给传入参数value，未找到直接返回false

查找方式可以手写二分查找，也可以用标准库比如std::lower_bound,具体实现方式比较自由

注意区分内部节点和叶子节点的查找，具体实现可以在其对应的page页面中进行，重点要注意内部节点的查找，其key值对应的value是大于等于key的集合，如果小于要查找的key，则需要返回key - 1对应的value

Insert

Insert的实现也要依赖于上面写的Findleaf()函数，因为在插入的时候我们需要找到insert_key恰好大于的key，将其插入到key的后面

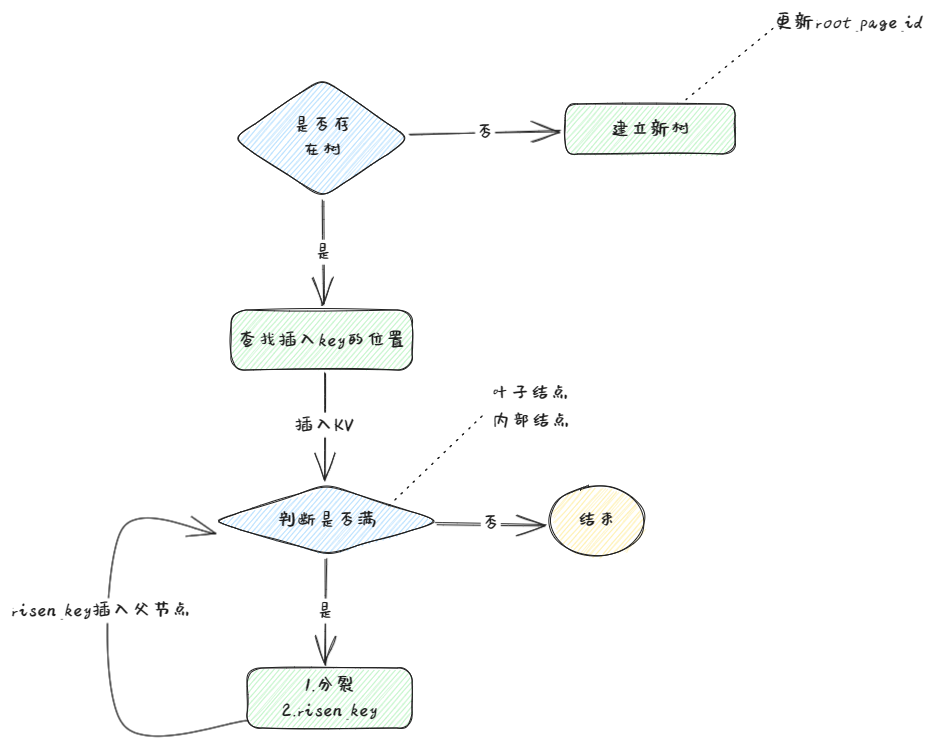
  1. 首先要检查是否已经存在树，只需要比对root_page_id是否等于INVALID_PAGE_ID即可，如果不存在，则建立新树，开始建立的树一定是leaf_page，最后不要忘记更新root_page_id
  2. 若已经存在树，则需要通过GetValue()中实现的FindLeaf()函数，找到需要插入键值对的叶子节点，直接插入（为什么可以直接插入？可以通过BusTub B+Tree Printer 看出，叶子节点一旦达到Maxsize便立刻执行分裂操作，即叶子节点一定有空余空间插入一组键值对）
  3. 插入之后需要判断叶子节点是否已满，若未满，则插入流程结束
  4. 若叶子节点已满，则执行分裂。分裂过程无非是新建一个叶子节点，将叶子节点分成两个满足半满的节点。一般我们将新节点作为该叶子节点的右邻居节点，所以直接将后半部分copy给right_neighbor_node，注意不要忘记risen_key,新生成了一个节点，新节点的第一个键值将上升至父节点中，此时需要再对父节点是否达成分裂条件进行判断
  5. 内部节点的分裂条件和叶子节点不同，内部节点的键值对可以占满整个page，换句话说就是当内部节点要插入时，没有足够的空间了，在这种情况下内部节点才会进行分裂，而不像叶子节点一样，一旦达到maxsize立刻分裂。所以内部节点的分裂需要先为其开辟一段能容纳下新键值对的空间，再进行插入流程，插入完成后，再将新page中的键值对像叶子节点一样，copy给新内部节点，此时，由于存在新的内部节点，该内部节点的第一个key将上升至父节点（内部节点），再对其父节点进行判断，依次递推，直到节点不需要分裂（未满）为止

notes：

分裂过程中，原节点的值其实不需要变动，只需修改节点的size即可，之后如有新值会直接覆盖掉

risen_key在叶子节点和内部节点中也不同，叶子节点是array[0].first,内部节点是array_[1].first

插入操作其实也不是非常复杂，remove要比insert更为复杂一些

Remove

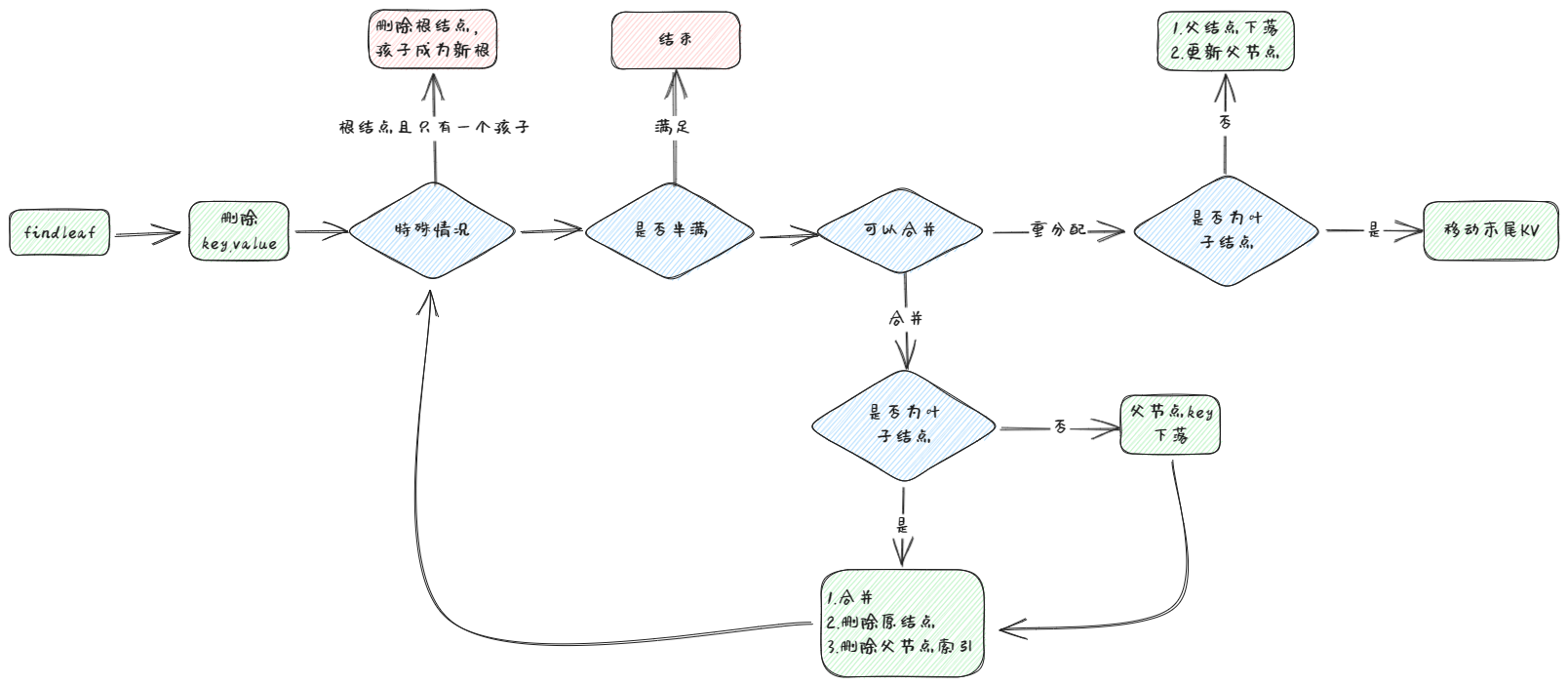
  1. Remove和Insert一样首先要拿到进行删除操作的叶子节点，直接进行删除操作，此时要考虑删除节点是根节点这一特殊情况，如果是根节点且恰好只剩一个孩子，那么这个根节点就没有存在的意义了，所以要让其only_child成为新根。

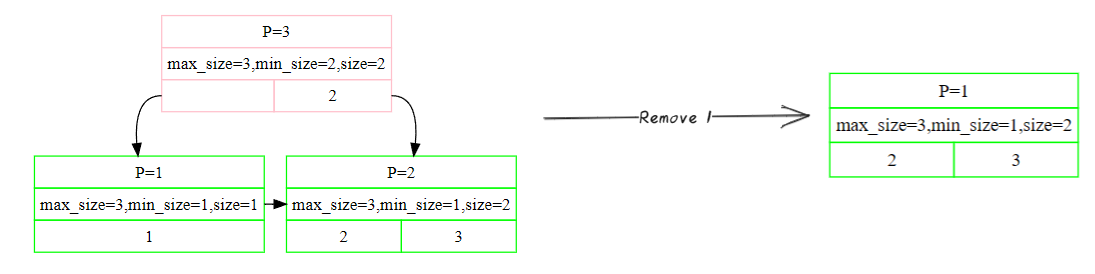
  2. 如果不为特殊情况，则对进行删除操作的节点进行判断，是否满足半满条件（注意叶子节点和内部节点的半满条件不同），若满足，则可以直接结束

  3. 如果不满足半满条件，则需要进行合并(Merge)或者重构(Redistribute)，怎么判断Merge还是Redistribute呢？这里就是要拿到其邻居（前后都可以），判断能否容纳两个节点的项

  4. 如果不可以容纳两个节点的项，则进行重分配。即将前节点的最后一项copy到后节点的第一项，注意后节点的key要在父节点中更改（因为first_key变了），如果是叶子节点可以直接将后节点0号key上升，如果是内部节点就要复杂一些，因为内部节点不可以重复，所以就有fallen_key的存在，在copy之前要先将父节点对应的key下落至0号位置（虽然内部节点的第一个key值无效，但是不影响我们存储键值），再进行重分配，分配完成后再将后节点的0号key更新至fallen_key位置。同时，因为是内部节点，不要忘记修改其移动项的子页面，要将其所有子页面的parent_page_id更新。

  5. 如果可以容纳两个节点的项，则会进行合并。将节点内部项全部移动到其邻居节点中，将父节点中原本键值对移除（其实就是将所有原位置后KV前移一位，再修改一下size即可）。合并完成后，还需要进行递归操作，因为父节点的size改变了，所以有可能不满足半满条件，直到有一个父节点满足半满条件为止

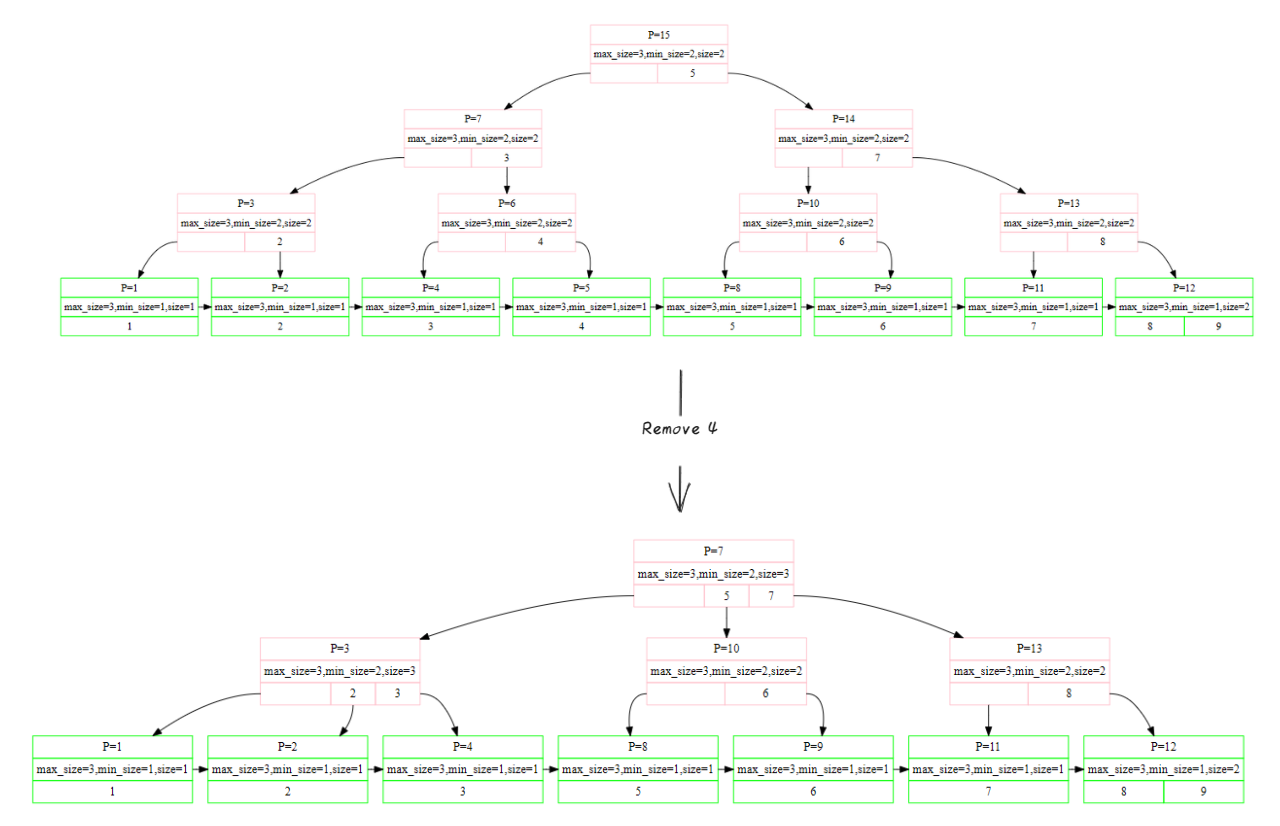
总体的删除流程就结束了

Debug && Sum up

虽然总体流程结束了，中途还会有无数个bug，尤其是当代码写的越来越长的时候，debug就成了十分折磨人的事情。但是善良的TAs为我们提供了一些用于debug的接口，可以在测试代码中利用Draw函数输出dot文件，将dot文件的内容贴到Graphviz Online 将树可视化，（你甚至可以看到每一步的树长什么样），再根据自己的树和测试样例进行比对，从而定位错误

也可以使用b_plus_printer来自行定义树，进行一些操作后来和官方给的可视化工具BusTub B+Tree Printer 进行比对，我当时就是用的这个方法加上打断点的方式定位到remove函数中的错误。

另外Insert测试样例中有用到迭代器的实现，可以忽略，也可以写上，毕竟不像B+树构造这么复杂，同时别以为本地测试样例过了就是成功了，因为checkpoint1的本地测试样例实在是太弱了（不光本地测试样例弱，我怀疑线上的测试样例也是本地的这几个），唯一有点点点难度的是ScaleTest，我看到好多人ScaleTest过不去，这个情况一般都是UnpinPage没有做好，多检查一下是不是Fetch之后忘记Unpin了。我当时remove函数实现有错误，提交到Gradescope上都显示全对，这个困扰了我很长时间，解决办法也是有的，下篇文章见！